MiNIMAL sURFACE TILING mETHODOLOGY
Prof. Haresh Lalvani and John Gulliford
In collaboration with SeokYoung Jung
This project required us to be open to failure and learn from it to proceed. Explorations usually resulted in more problems and questions instead of solutions. We conducted multiple tessellating brick studies on doubly curved topological shells.
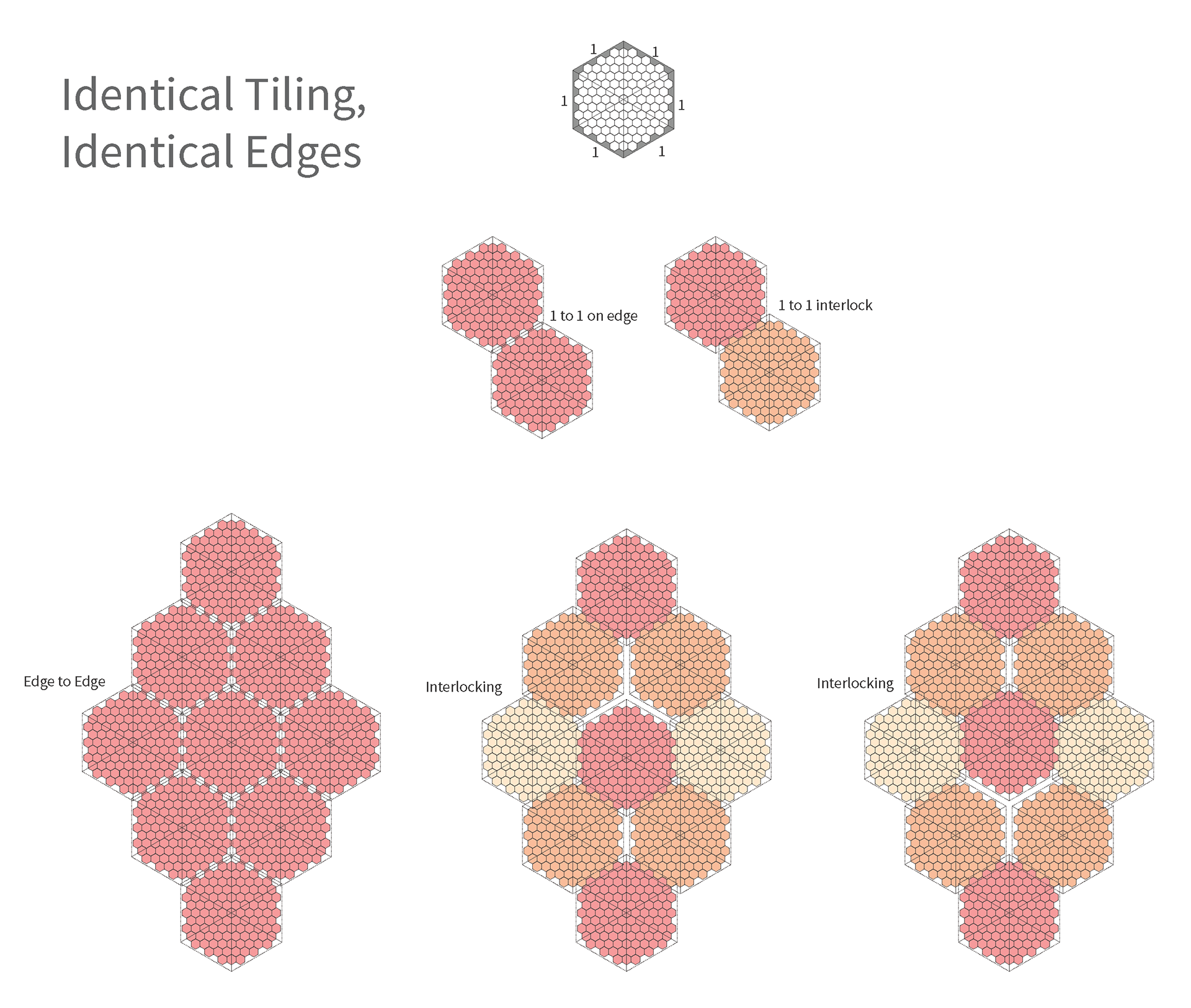
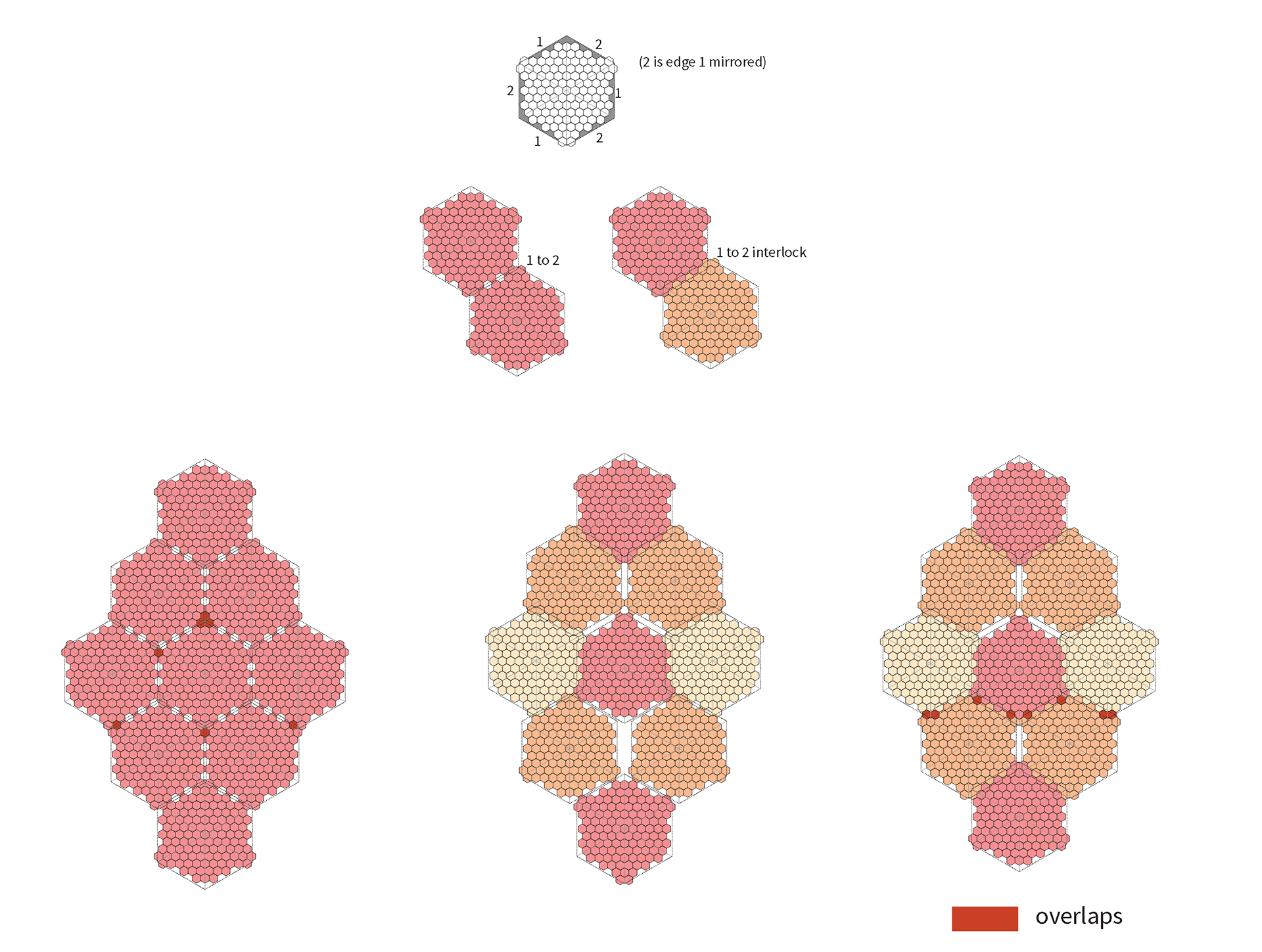
We used hexagon tiles as the tessellating bricks. Using one milled minimal surface mold, we explored multiple tiling methods to create a module and solve its edge conditions. Once a tiling method was deemed a success in a 3D study, I explored different edge conditions and possibilities of connections via 2D studies and further resolved them to make a physical final model.
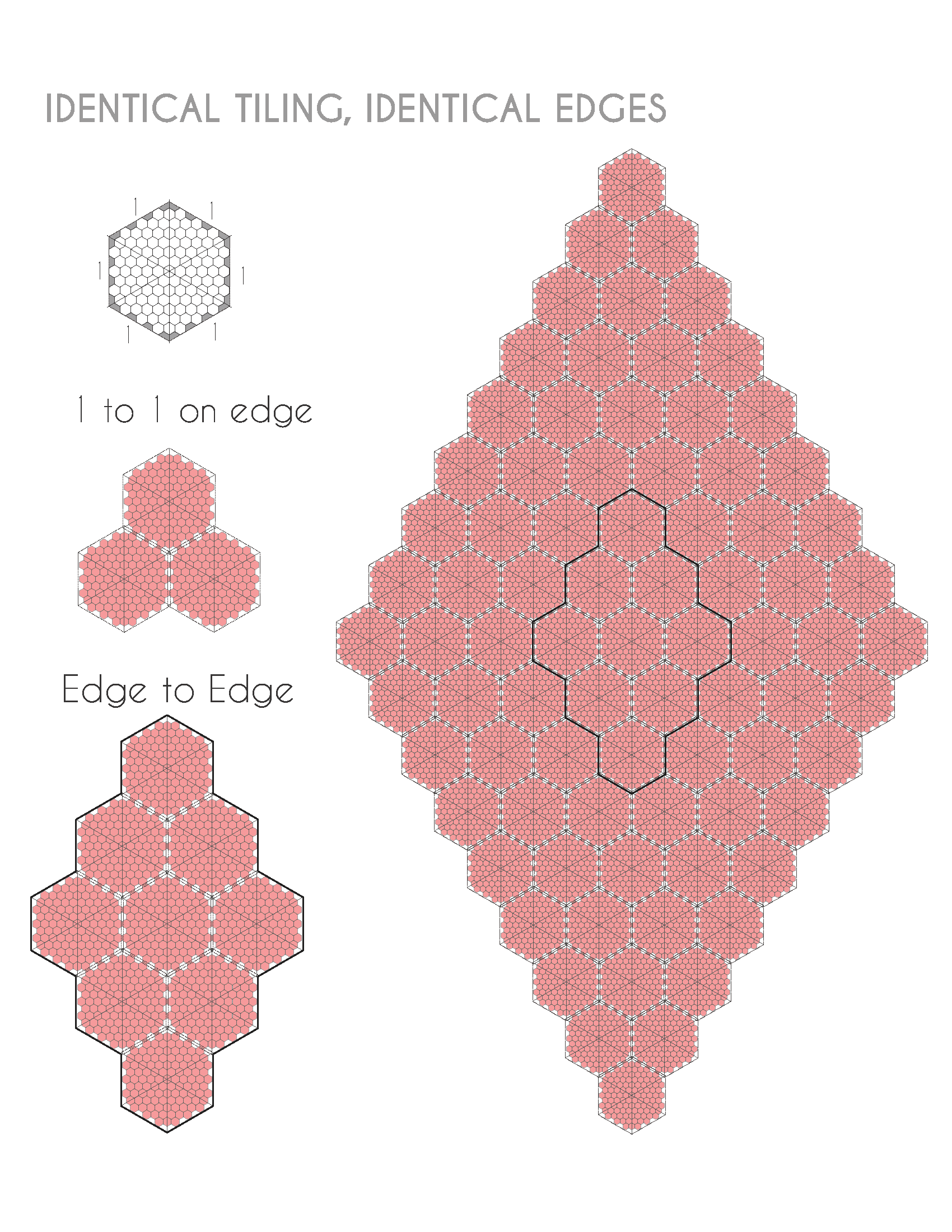
One big module consists of 9 identical small hex modules that connect edge to edge. The one big module can continue infinitely.
We used hexagon tiles as the tessellating bricks. Using one milled minimal surface mold, we explored multiple tiling methods to create a module and solve its edge conditions. Once a tiling method was deemed a success in a 3D study, I explored different edge conditions and possibilities of connections via 2D studies and further resolved them to make a physical final model.
One big module consists of 9 identical small hex modules that connect edge to edge. The one big module can continue infinitely.
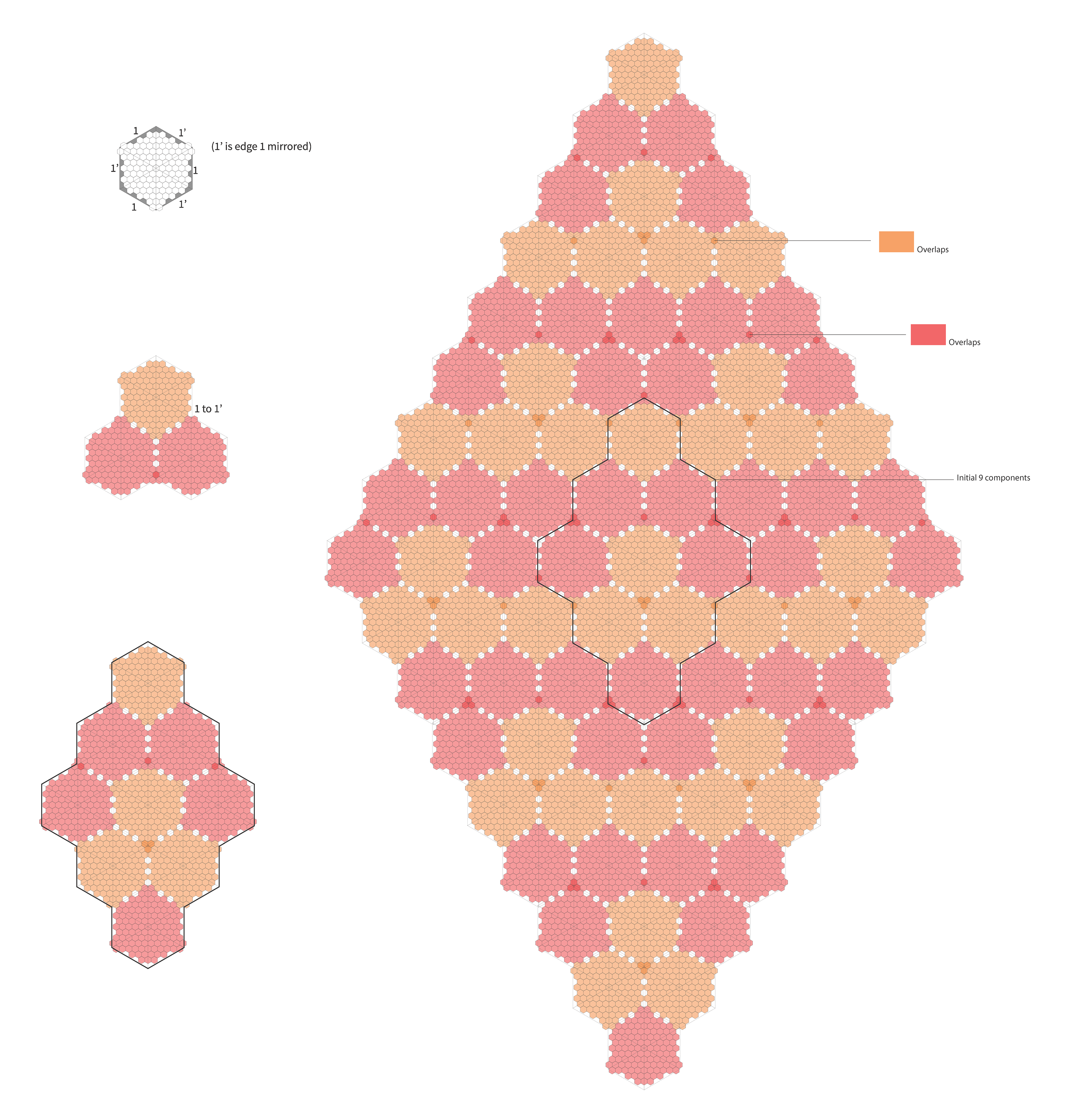










schwarz surface
Prof. Haresh Lalvani and John Gulliford
In Collaboration with Khadeeja Boriyawala, Safa Mehrjui, SeokYoung Jung, Celine Lee, Diyang Shen and Huaiben Yang
Schwarz surface with 3d printed connections, wired edges, and stretched fabric for rapid assembly. This was a group project where I took on a project manager roll. I coordinated between the professors and my team to best understand the project needs, deliverables, and schedule. Once we decided on this minimal surface to develop as a prototype with minimal support frame, I created the digital model using rhino and grasshopper. I coordinated between my teammates to assign further developments of the connection nodes that were to be 3D printed and assemblage of other materials such as wire and fabric.
This project really taught me the value of teamwork as it was a success only as a result of great coordination between all my peers.


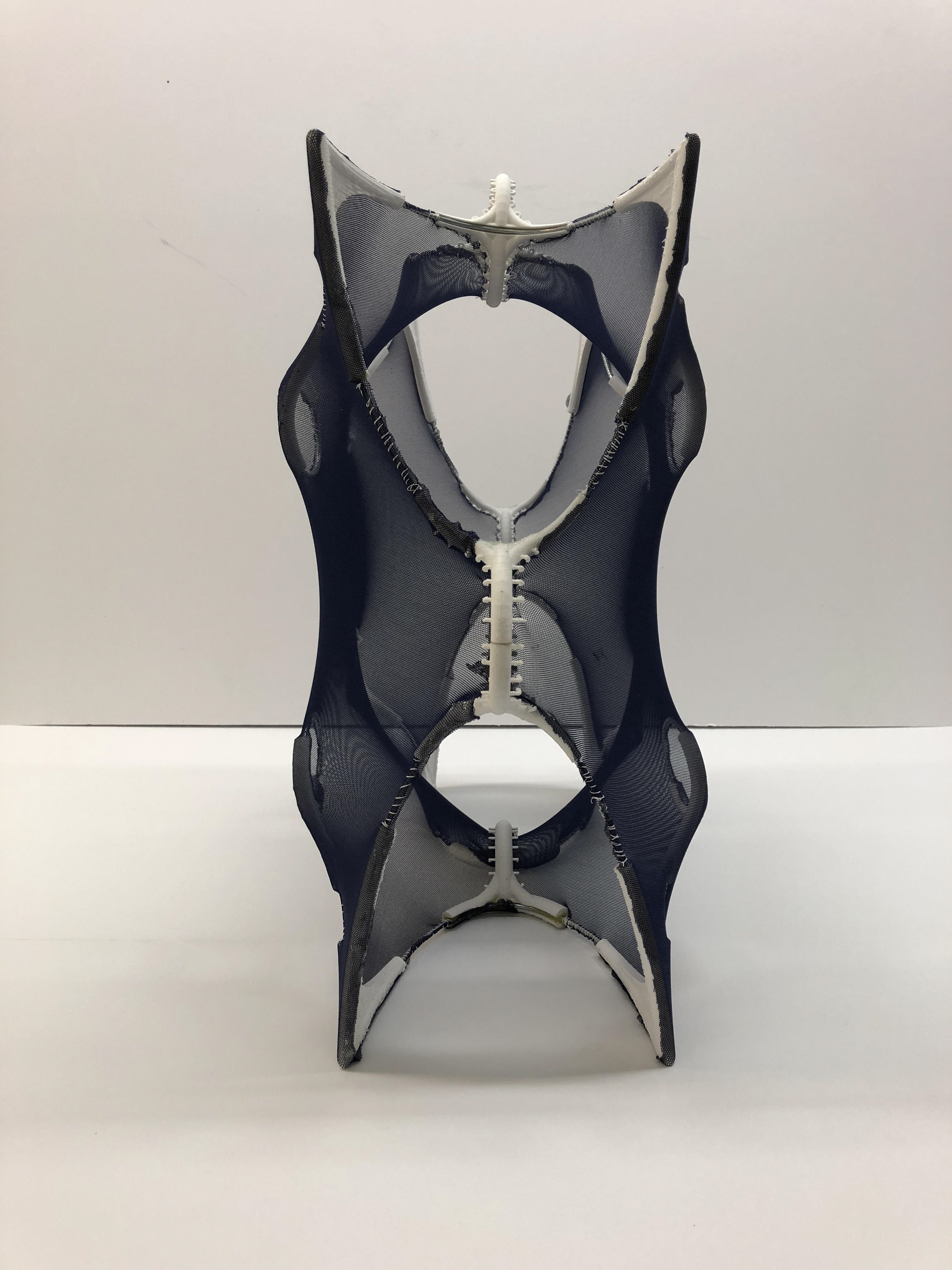





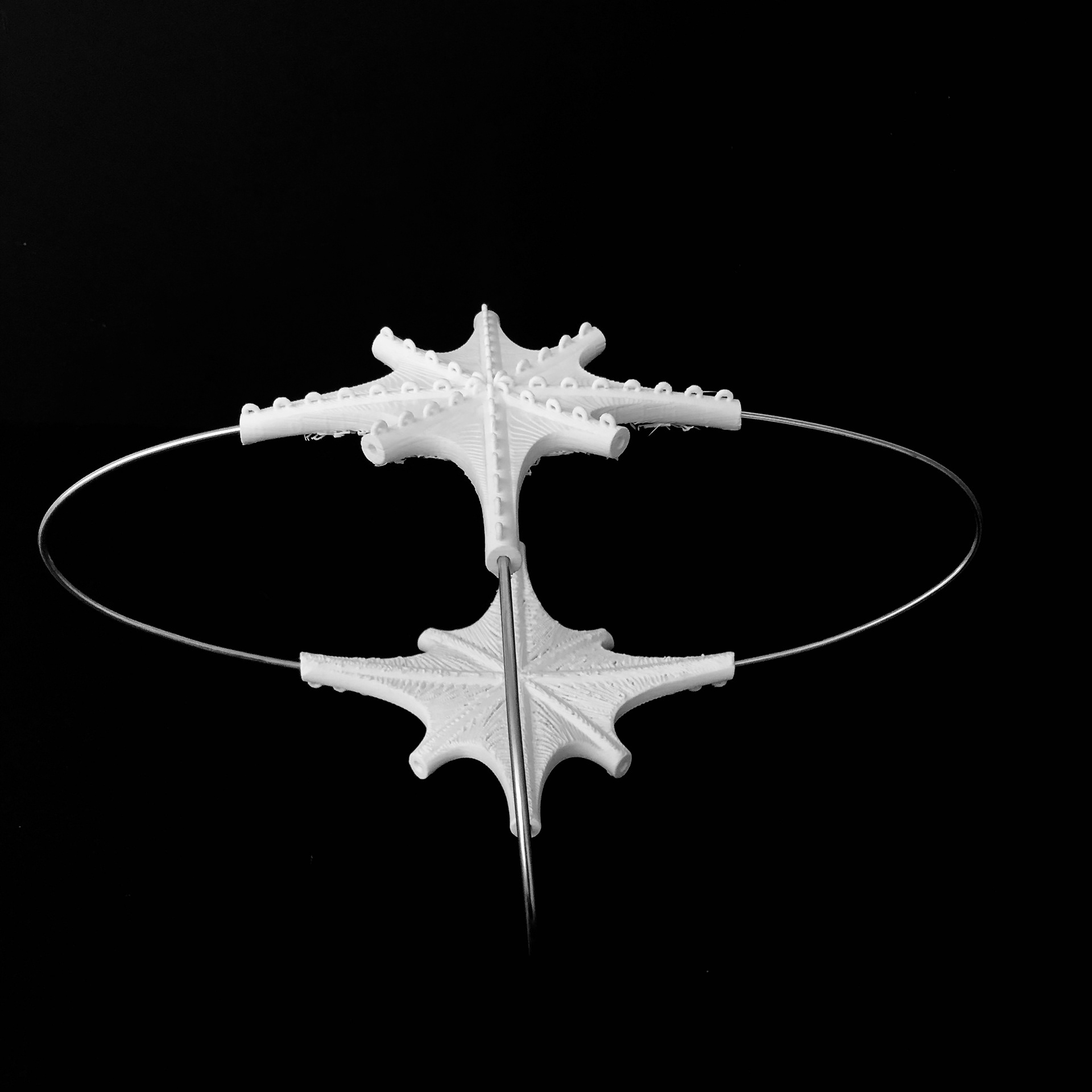
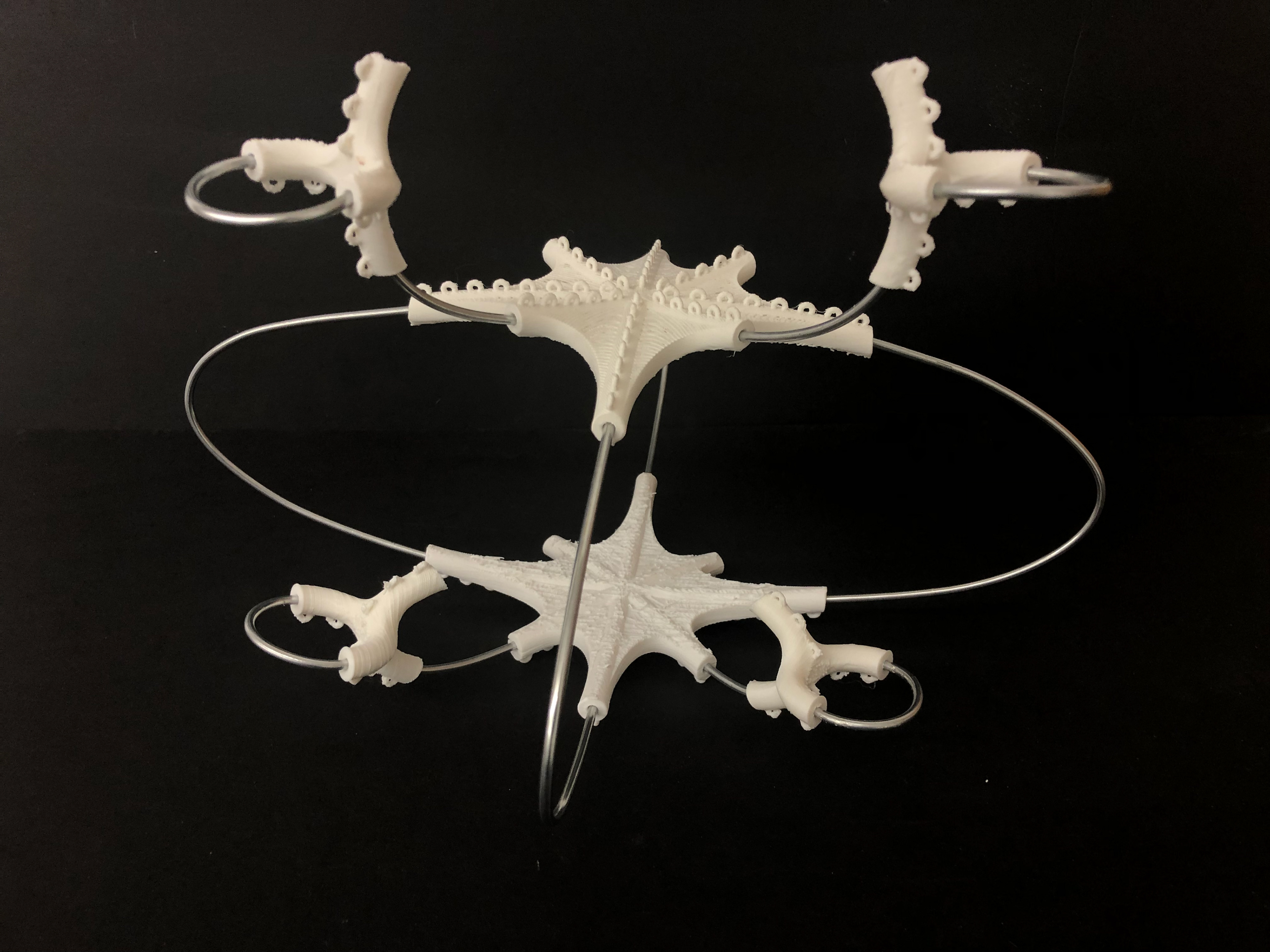








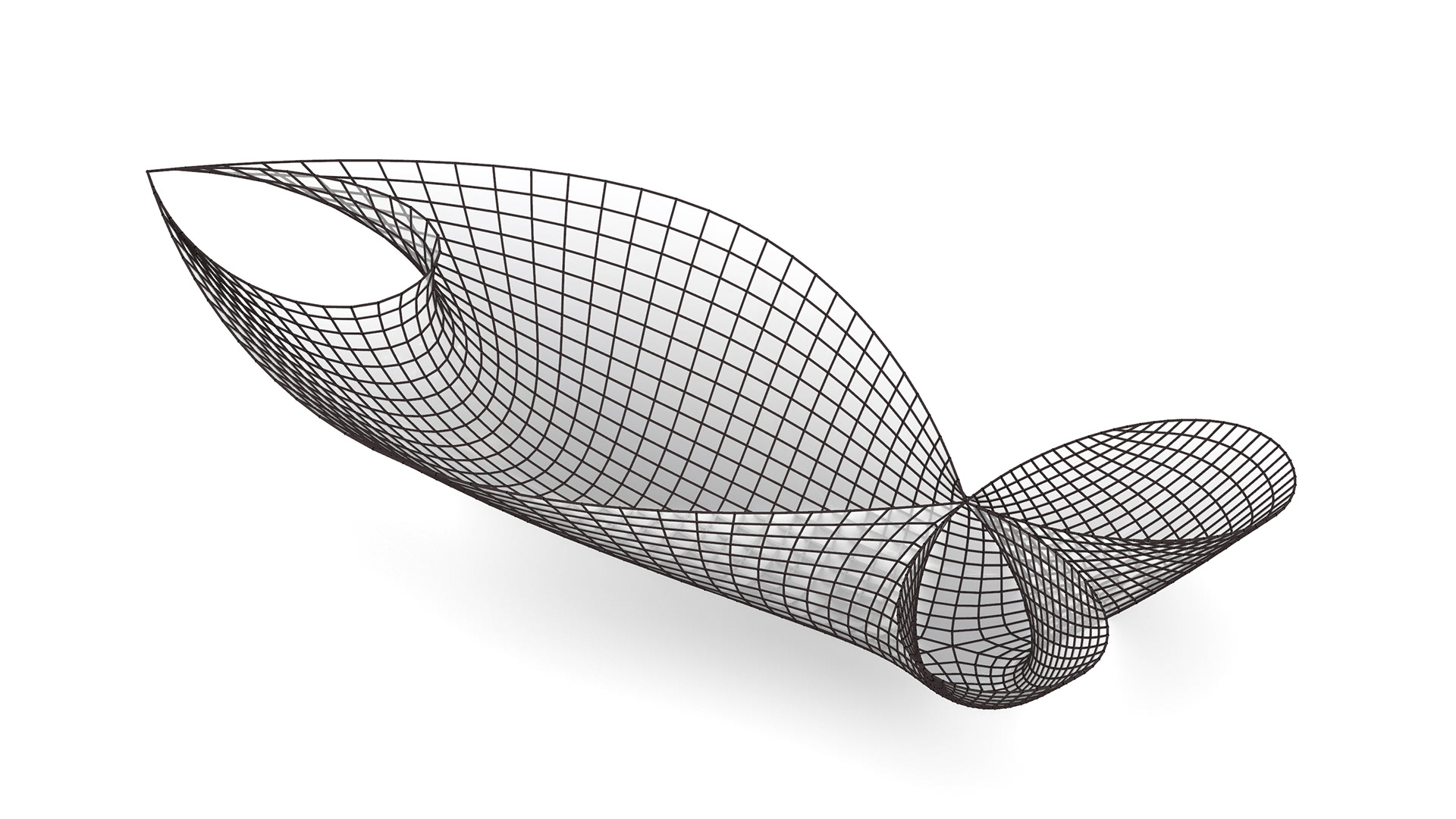
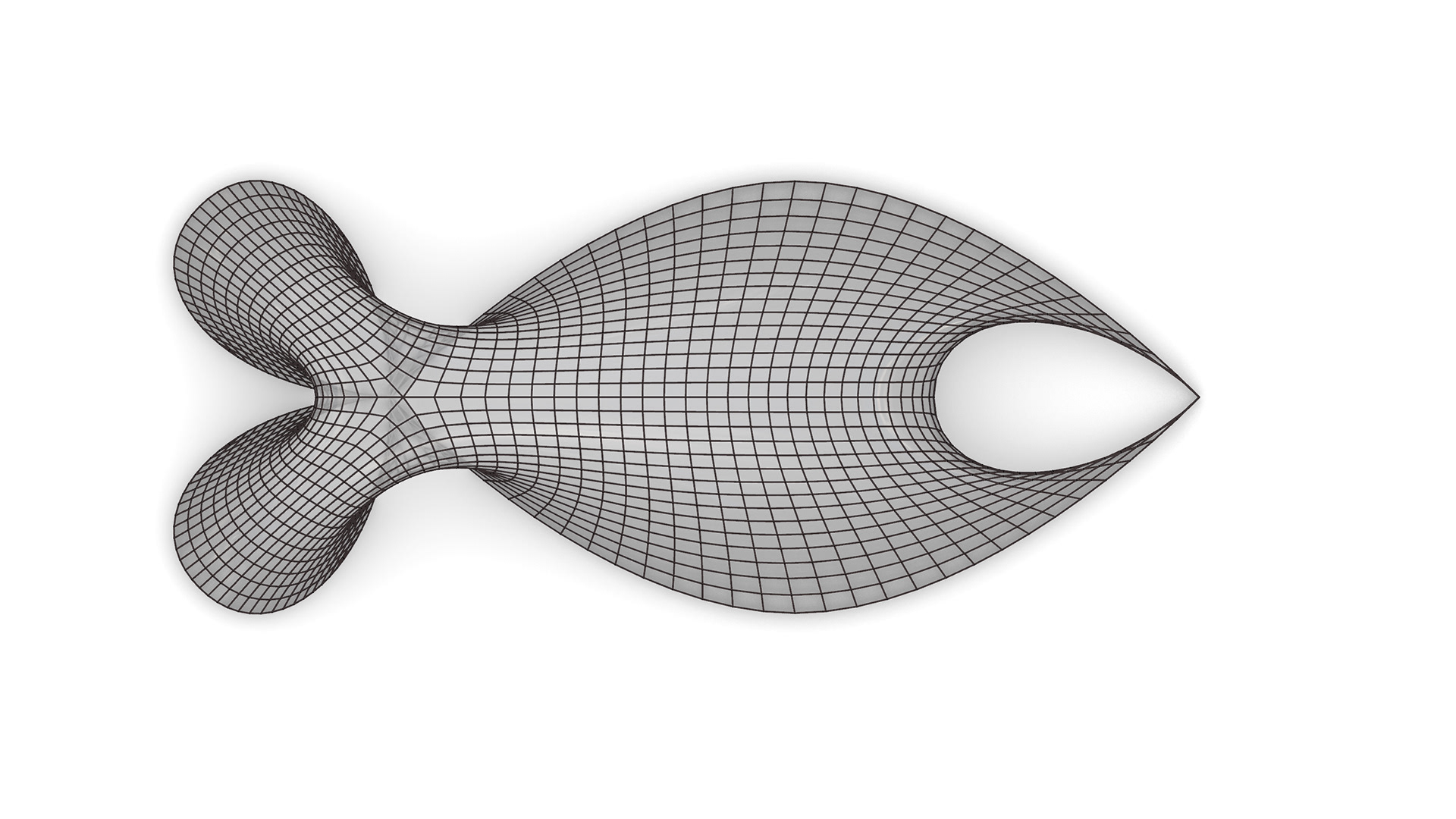
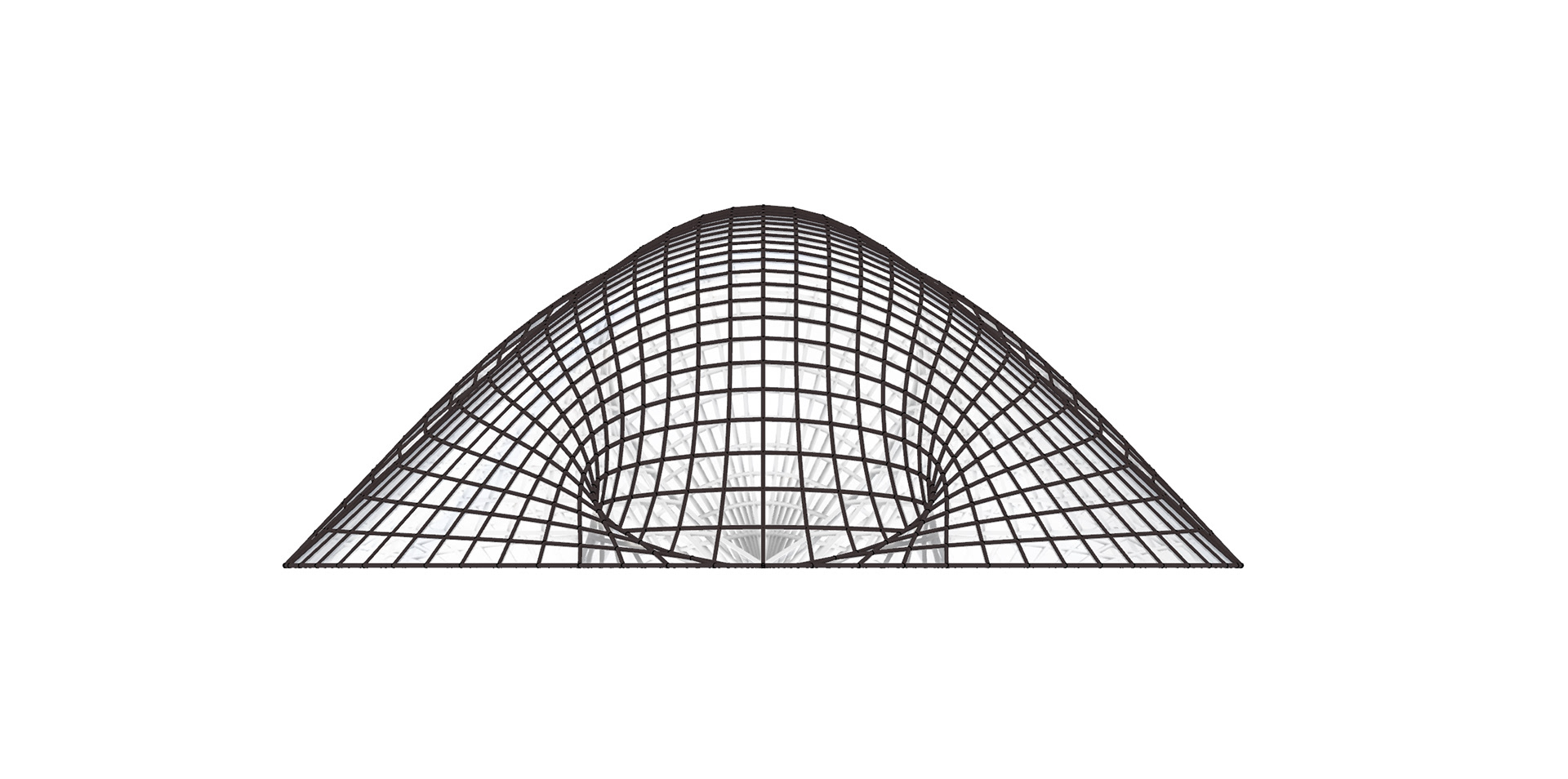
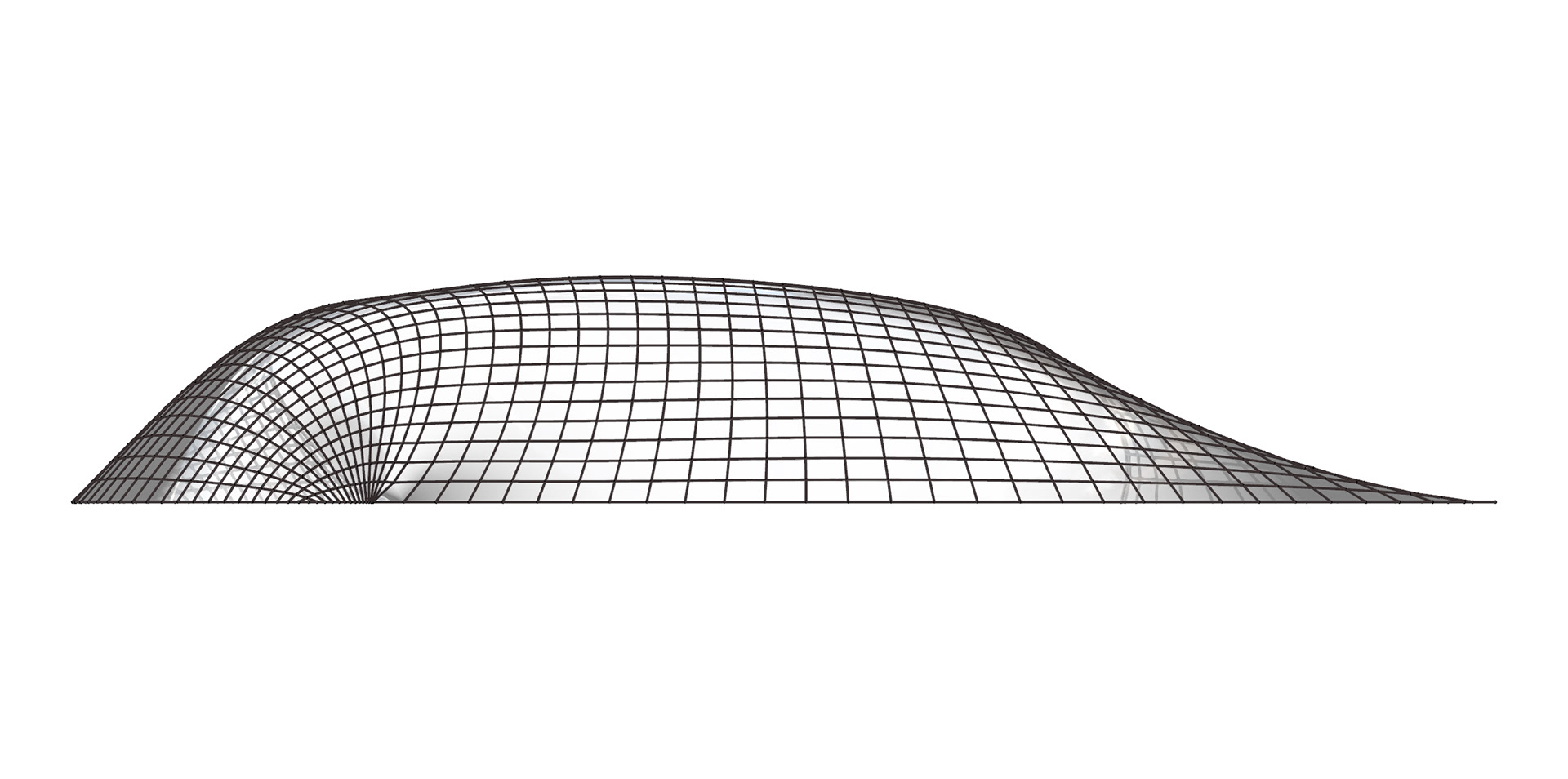
SINGULARITY SHELLS
Research Assistant to Prof. Haresh Lalvani
Summer 2019 - Summer 2020
The shell shown here is one of 8 singularity structures that are conceived as gravity-formed surfaces. These surfaces are reversed as grid shells using the method invented by Frei Otto. The render on the right show interior views of large-scale singularity grid shell and its different views. As a research assistant, I learned how to model these shells using rhino and grasshopper scripts. Throughout this project we came across problems that were not solved ever before. Therefore, a lot of innovative problem solving was required where I learned that failure is key to success. Through this research emerged a new grid that can be used in
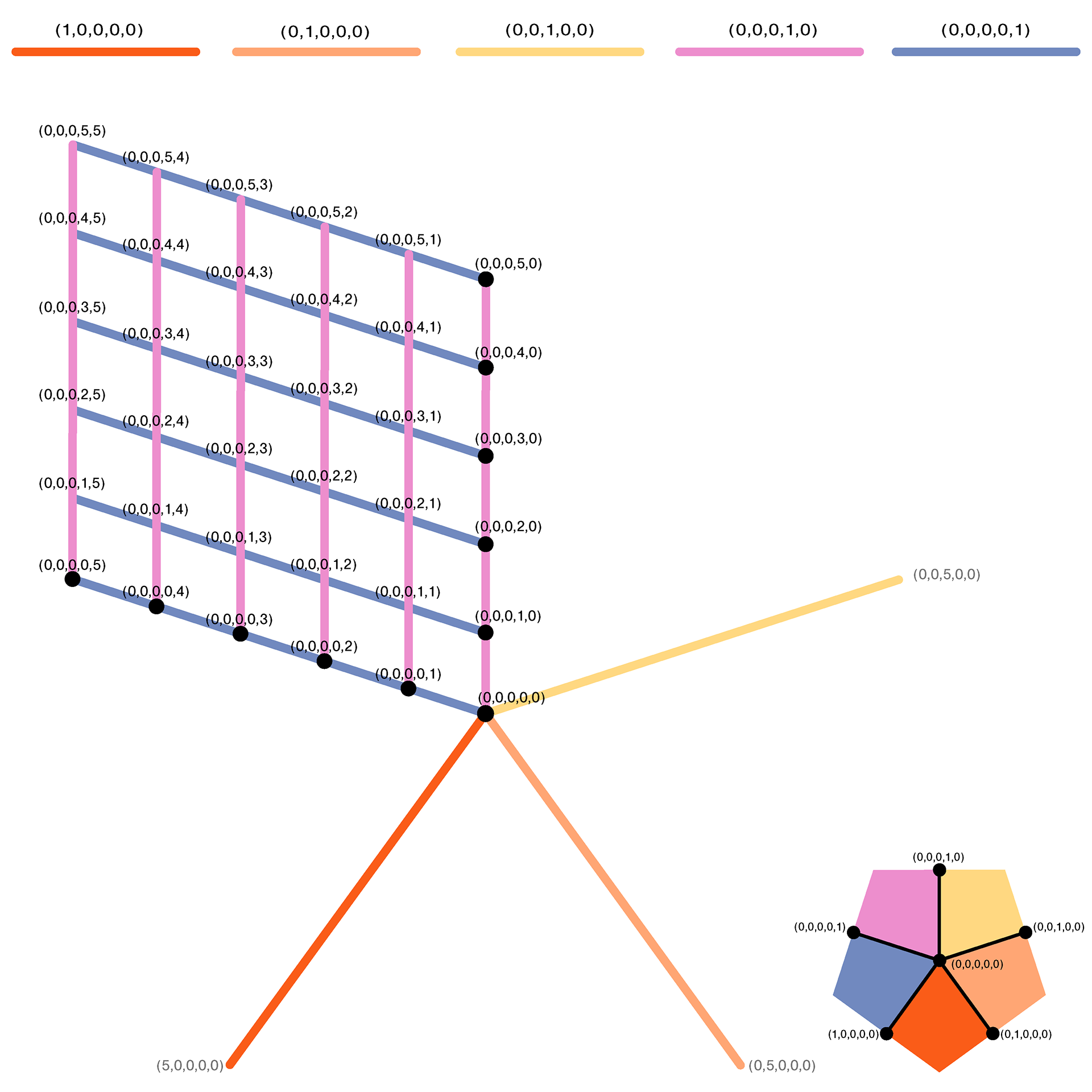
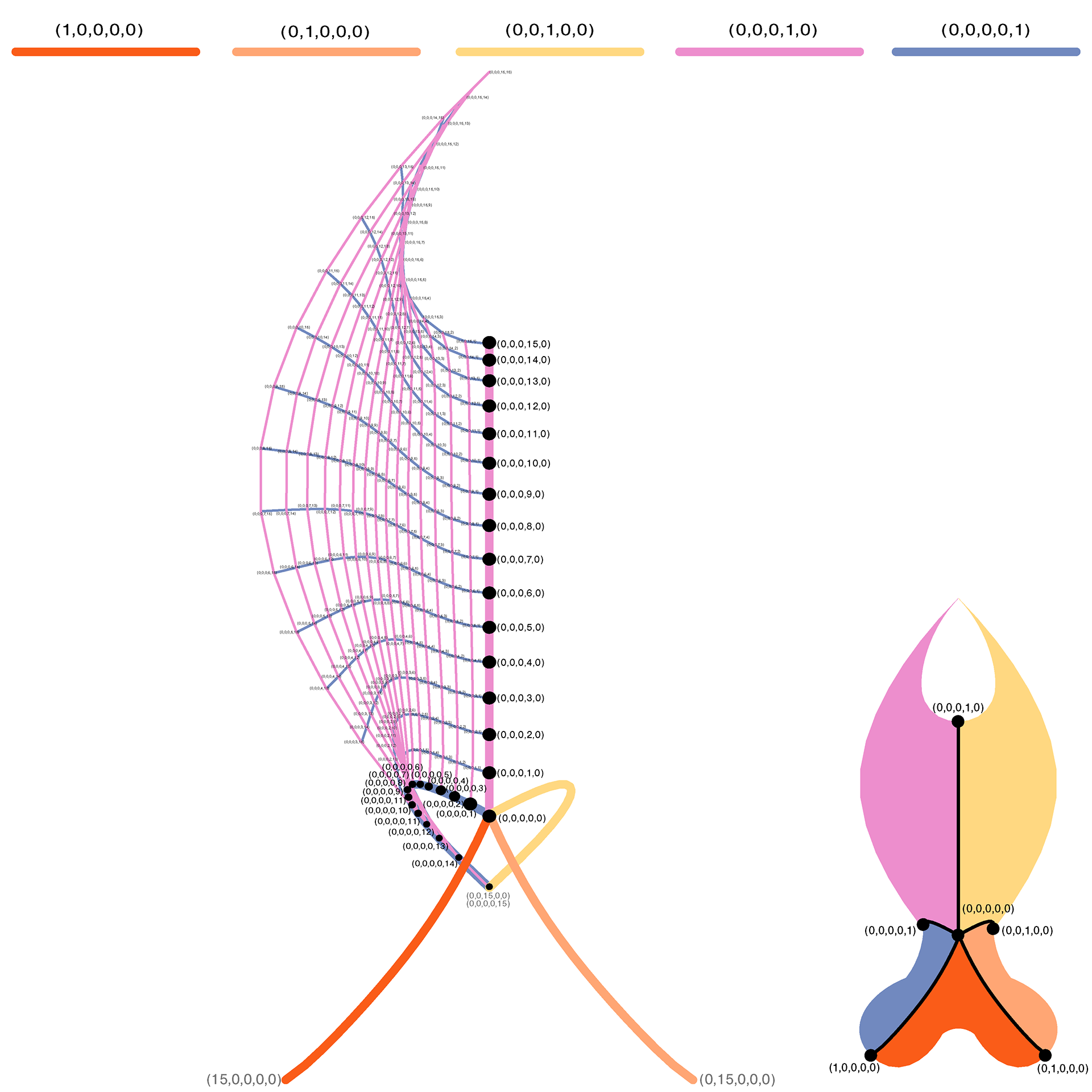
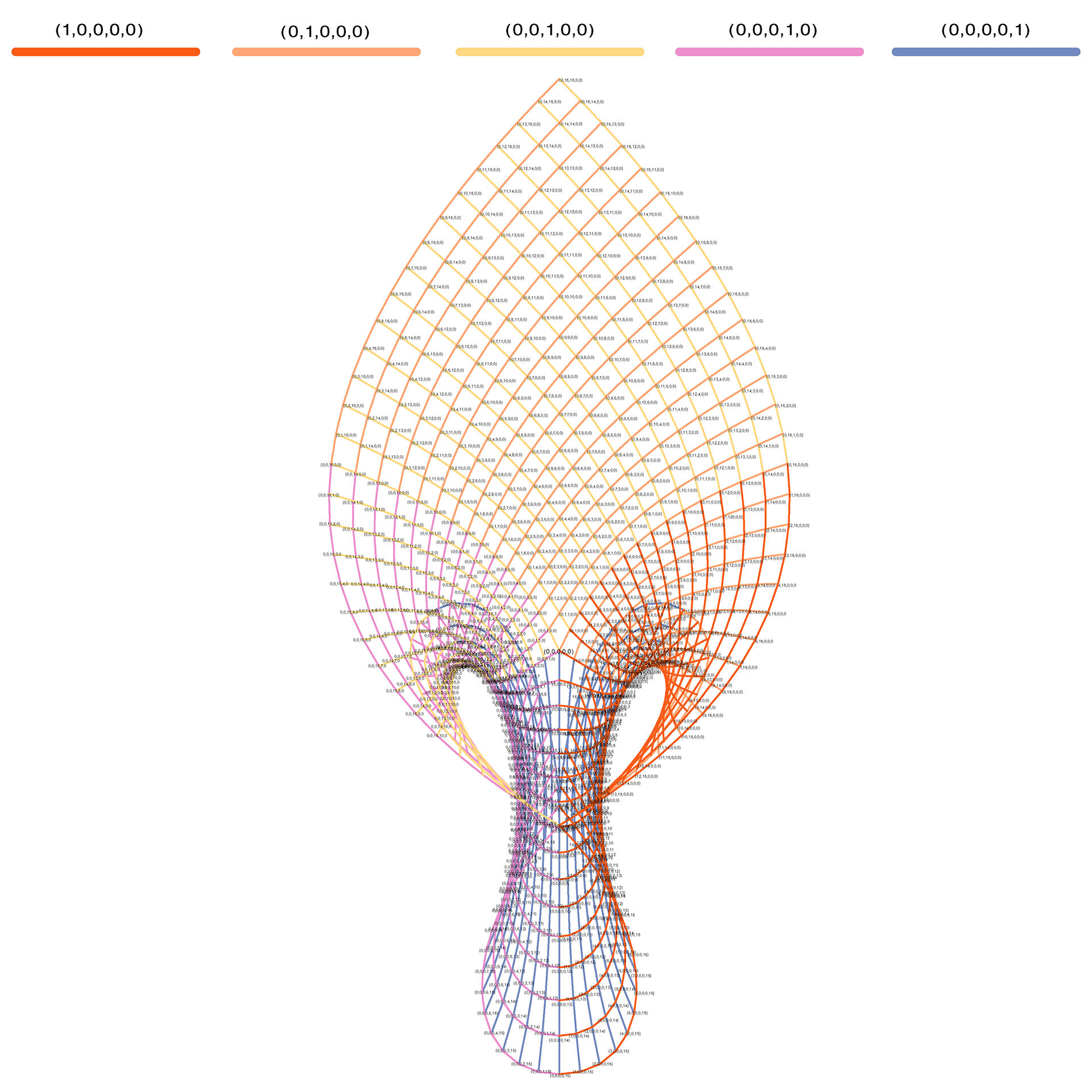
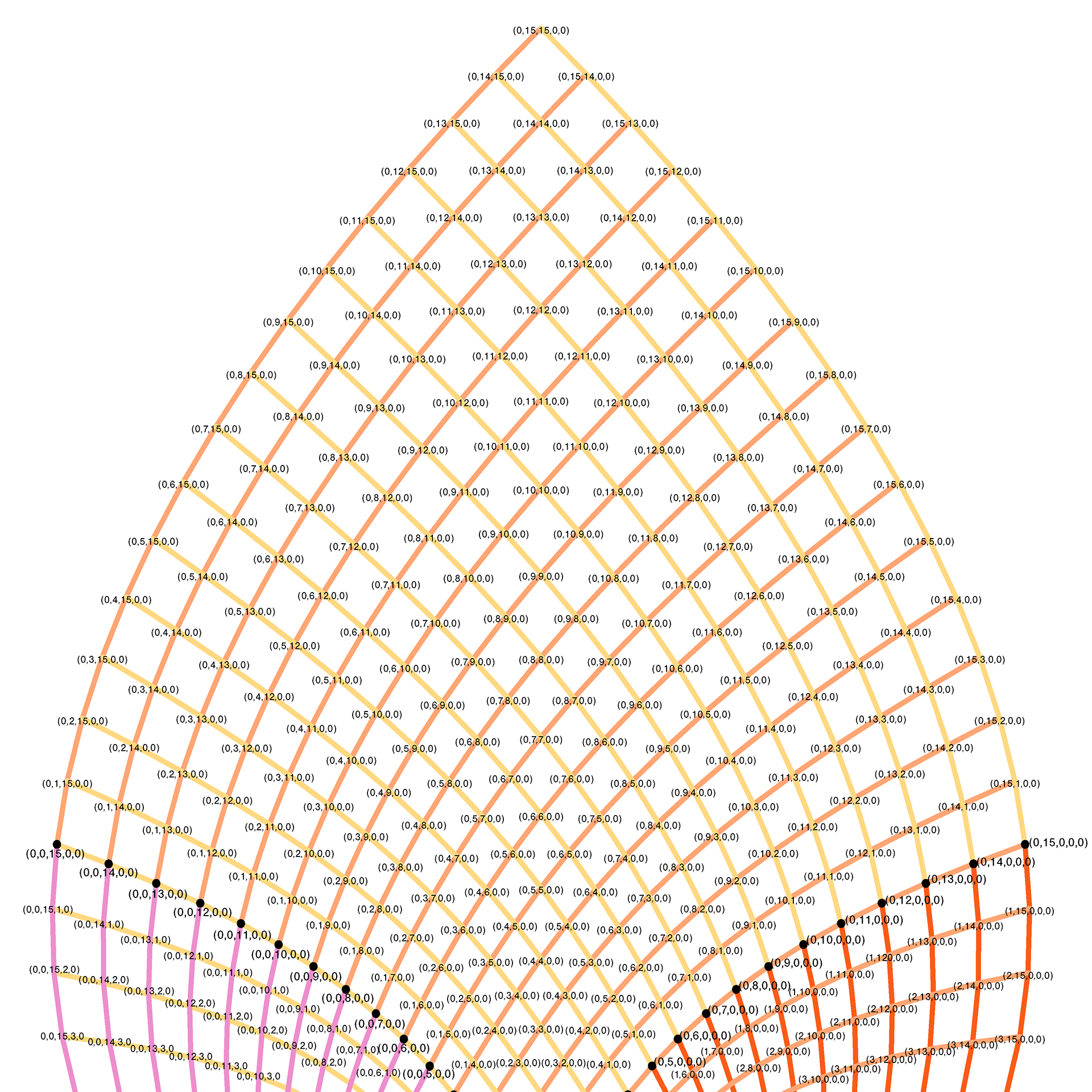
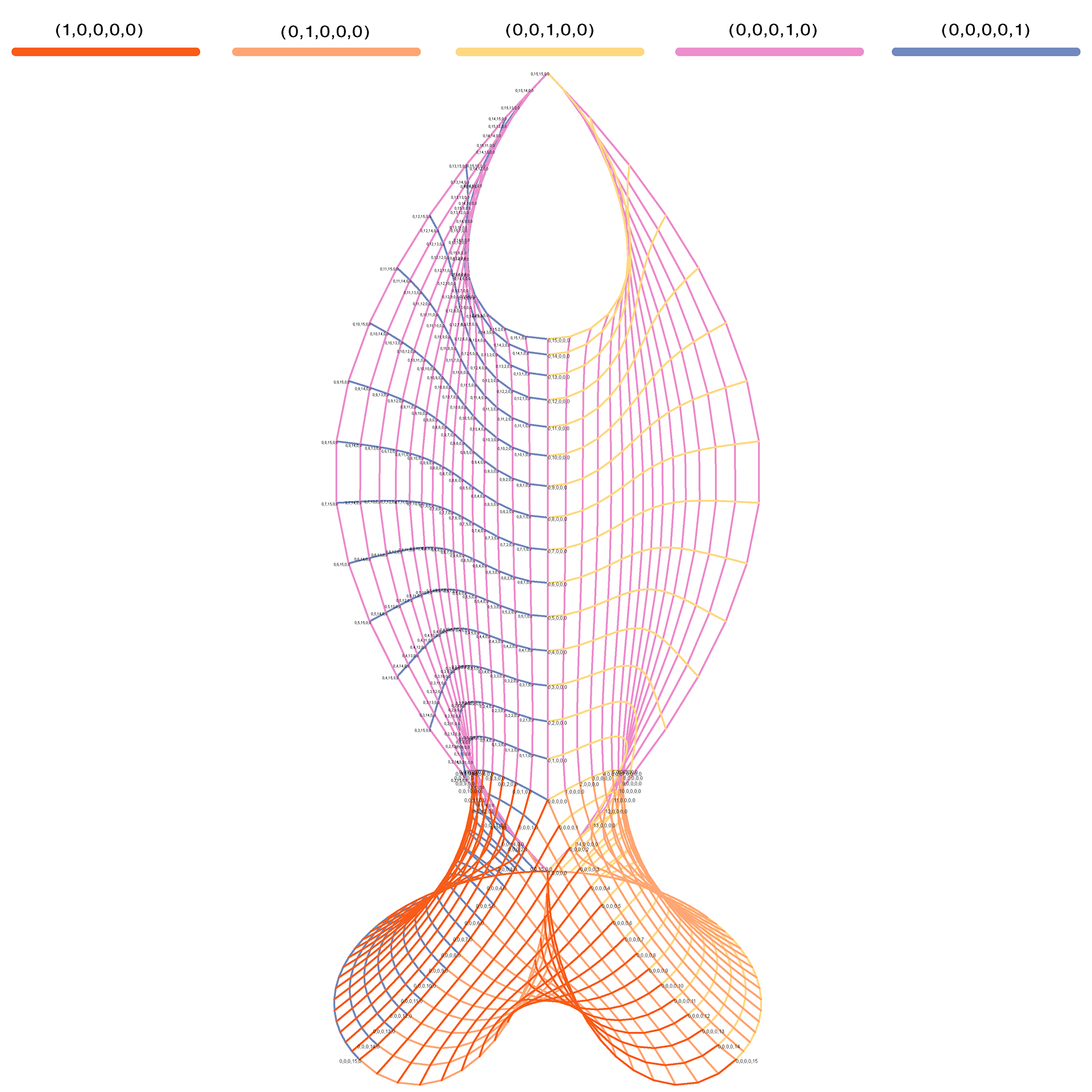
computational construction. Instead of just 3-axis grid, this is a 5-axis grid. To the right is an example of a 5-axis grid applied to a quad of a singularity grid shell.
computational construction. Instead of just 3-axis grid, this is a 5-axis grid. To the right is an example of a 5-axis grid applied to a quad of a singularity grid shell.